timelets

I keep coming back to this video about the relationship between (pre-)sheafs and cohomology. Here he says that "the number one technique in mathematics is turning any problem into a linear algebra problem.

More generally, Lawvere often talks about mapping geometry to algebra.

https://youtu.be/RPuWHN0BTio?si=U0h7YM-3GlcyvnS5&t=1890

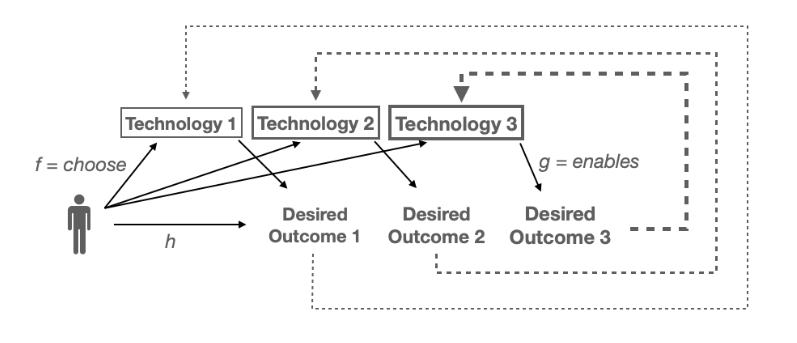
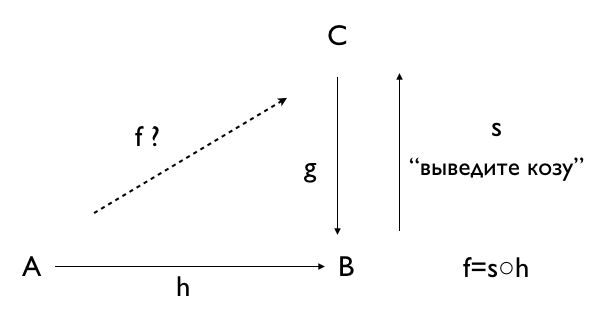
D --> J <-- T ( c: D --> T is the solution to a choice problem, per Lawvere).

d: D --> J
e: T --> J
c: D --> T

This diagram is a regular Kan extension problem, with a cohomology twist, i.e. assigning values to both objects and arrows.

...dynamic processes give rise to particular growth patterns: branching out whilst foraging (to maximize coverage of territory) and forming networks once nodes have been established (to strengthen connections and facilitate the transfer of information). Branching is a fundamental strategy within myriad biological organisms and physical phenomena, from the bifurcation of river deltas, lightning strikes, tree roots and branches, to mycelial networks and in our own bodily systems including blood vessel networks and the cross channelling of neural pathways. Branching facilitates ‘the transmission and parsing of information, no less than the transfer and dissipation of energy’ and, according to philosopher Stephen Shaviro, ‘is an essential process of Nature’ (Shaviro, 2016: 220).

Drawing Processes of Life, 2024.

Again, branching and consolidation can be represented as critical points in Morse-Smale theory. https://timelets.dreamwidth.org/1568281.html

In a narrative, a character can create a branch, thus diverting the flow of events to their advantage or disadvantage. For example, in the LRRH fairy tale the Wolf diverts the girl's attention to beautiful flowers and gains power over her future. It takes magic to undo his villainy.
An example of a positive diversion would be Царевна-Лягушка, where the ugly frog bride tells the prince to get some sleep while she takes care of the king's challenge.

In social theory, topology-based approach to agency can help model the difference between democratic elections and sociological polling for potential course corrections in authoritarian regimes, like the Putin's (see, e.g. Spin Dictators, by Guriev and Treismann).

M&A narratives and consequences can be treated the same way.

upd. Kan extensions/lifts can be used to represent branching/consolidation patterns.

upd 1. Does it apply to Lawvere's Hegelian Taco?

1 --> T1  --> T2
        \     /\
         \    |
          \   |
          _\| ]
             P

In the beginning...

e: 1 -> T1 is an equalizer
f: T1 -> T2
g: T1 -> P
h: P -> T2

f = h g

T1 is a narrative
T2 is an enablement

Smuggling in the Kan extension for dummies.

When in doubt build a model based on the Kan extension. Or at least, use Lawvere's simplified version of it ( determination/choice).

* Questions (A) -> Little Red Riding Hood (B) -> Learning [Wolf Detection] (C)

A -> C maps to False ( A -> Ω), which hints at the idea that marginal knowledge can be modeled as a topos. We can also show the nature of the transition from Google Search to GPT.

* All objects are marginal.

I think I'm getting the hang of the Kan extension concept. For example, the future, at least in technology, seems to be a left Kan extension, while the past and the present would be the right one. This is just an initial idea I and sill need to develop a proof with specific examples, using the system model.

In the meantime, I"m hoping to finish the first draft of the book by the end of this year. It looks quite doable because I'm already halfway through the Cinderella part, which should be next to last.

https://www.youtube.com/watch?v=xTVSMJhDoOQ

Technology toolkit re-use is an extension problem. E.g. Julius Cesar's guide for building army camps using common agricultural approaches of the time. The use of steam engine manufacturing toolkit for railroads, steam ships, etc.

Technology choice or development is a lifting problem. E.g. discovery/choice of the right data set for a desired ML application (see IBM's recent failure vs TikTok's success).

In the LRRH narrative we see the failure of an existing solution to the extension problem, i.e. the werwolf destroys the girl's ability to deliver the medicine to her grandma.

“ ...to learn is to form an internal model of the external world.”

--- Stanislas Dehaene. “How We Learn.”

Note that he either externalizes confirmation of the model or considers its confirmation to be a part of formation. (upd. via trial and error).

cf: Lawvere's rough sketch of mathematical thinking where confirmation can be made explicit.

Implicitly, Lawvere & Schanuel make a good case for using Kan extensions in science.

For some reason, I understand (imagine) the right Kan extension much better than the left one. Really weird.

Под утро приснилось, что анекдот "Выведите козу" можно привести как пример Kan extension. Надо подумать.

Thus Kan extensions are simply a method for taking two functors and coming up with a third functor that attempts to make a certain triangle make sense. Requiring this triangle to be commutative is too restrictive, so instead Kan extensions rely on natural transformations to help make the extension be the best possible approximation of F along K.

--- Marina Christina Lehner.

S	M	T	W	T	F	S
1	2	3	4	5	6	7
8	9	10	11	12	13	14
15	16	17	18	19	20	21
22	23	24	25	26	27	28
29	30

Entries tagged with kan

(no subject)

(no subject)

(no subject)

(no subject)

(no subject)

(no subject)

(no subject)

(no subject)

(no subject)

(no subject)

Kan extension for comedians: "выведите козу"

(no subject)

(no subject)

Profile

June 2025

Syndicate

Most Popular Tags

Page Summary

Style Credit

Expand Cut Tags