![[personal profile]](https://www.dreamwidth.org/img/silk/identity/user.png){kind=small}
(no subject)
Mar. 7th, 2021 06:37 pmUsually the key aspect of an action of some is that itself carries an algebraic structure, such as being a group (or just a monoid) or being a ring or an associative algebra, which is also possessed by and preserved by the curried action . Note that if is any set then is a monoid,
https://ncatlab.org/nlab/show/action
also see Lawvere, 1986
===
MxA-> A
UxA -> A
https://ncatlab.org/nlab/show/action
also see Lawvere, 1986
"Historically the notion of monoid (or of group in particular) was abstracted from the actions, a pivotally important abstraction since as soon as a particular action is constructed or noticed, the demands of learning, development, and use mutate it into: 1) other actions on the same object, 2) actions on other related objects, and 3) actions of related monoids. "
===
MxA-> A
UxA -> A
(no subject)
Oct. 27th, 2020 11:39 pmThere's definitely a case for Crazy being a right adjoint to Stupid (left adjoint). For example, in the Three Little Pigs story the Wolf is a right adjoint, while the construction mess before that is the left adjoint.
Something like that:
Wolf: Pig x Pig -> Pig
Good Old Days: Pig -> Pix x Pig ( diagonal functor).
Similarly, Prince is a right adjoint to Cinderella.
Something like that:
Wolf: Pig x Pig -> Pig
Good Old Days: Pig -> Pix x Pig ( diagonal functor).
Similarly, Prince is a right adjoint to Cinderella.
Past and Future as adjoints
Aug. 31st, 2020 09:21 amIn a two-level past-future transition, we get two different transition functions f (what is going to be there) and g (what is not going to be there). We also get two triples of adjoint functors, depending on how we construct a fibered domain of the past (product vs coproduct).
Lower-level past and future are modeled as exponential objects.
Setpast -> Setfuture
(no subject)
Mar. 24th, 2020 06:57 pmOur deepest insights must—and should—appear as follies, and under certain circumstances as crimes, when they come unauthorizedly to the ears of those who are not disposed and predestined for them.
--- Friedrich Nietzsche, Beyond Good and Evil.
I've been thinking how to express formally the idea that the future as Crazy and the past as Stupid form adjoint functors. This is another instance of the same thought that circumstances make deep insights appear as fillies, i.e. crazy.
(no subject)
Dec. 3rd, 2019 01:48 pmI've long suspected that Crazy and Stupid perceptions of the Other (applies to historical times, mindsets, etc.) form an intrinsically connected pair. In Category Theory they can be modeled as adjoints with specific meanings; that is, Stupid would be Forgetful, while Crazy would be Free.
https://www.youtube.com/watch?v=Ro8KoFFdtS4&feature=youtu.be&t=3460
re: https://chasovschik.livejournal.com/1258817.html
https://www.youtube.com/watch?v=Ro8KoFFdtS4&feature=youtu.be&t=3460
re: https://chasovschik.livejournal.com/1258817.html
(no subject)
Mar. 11th, 2018 10:37 am
And similarly for functors, the effect of U is described by simply erasing some parts of the diagrams (which is easier to demonstrate with chalk!).
-- Steve Awodey. Category Theory, 2010. pp 22-23.
The chalk idea is absolutely brilliant! I tried this technique last night and it worked miracles to clarify my thinking.
Непостижимая эффективность крановщика
Feb. 18th, 2018 09:00 amЕсли собрать всех людей, которые создали подъемный кран, то они не поднимут 100 тонн. А крановщик поднимет. И будет поднимать каждый рабочий день, каждый рабочий год.
(no subject)
Jan. 9th, 2018 01:39 pmWhen reading "Capitalism without Capital" it's hard to escape the parallel between the partition of property into tangible/intangible and the partition of a human into body/soul.
upd. Любарский в "Рождение Науки" пишет, что классификация Линнея основана на том, что можно пощупать.
upd. Любарский в "Рождение Науки" пишет, что классификация Линнея основана на том, что можно пощупать.
(no subject)
Jan. 4th, 2018 04:42 pmОттуда же:
When we have two formal systems that are difficult to understand due to their idealization schemes the right functor can serve as an explanation. In this approach, adjoints would form complementary explanations.
Создавая формальный язык описания, схематизируя реальность, производя идеацию, наука создаёт область контринтуитивного и непонятного. Сколько выигрывается для экономии познания на формализации и кратком чётком обозначении идеализованных однородных элементов, столько теряется в понятности и требует времени для интерпретации, популярного изложения и обучения. Наука создаёт область ясного знания, и чем оно яснее, тем более удалено от обычного взгляда и здравого смысла.
Любарский, Г.Ю. 2011.
When we have two formal systems that are difficult to understand due to their idealization schemes the right functor can serve as an explanation. In this approach, adjoints would form complementary explanations.
(no subject)
Dec. 29th, 2017 11:08 amДопустим, я изобрел велосипед/bitcoin. Как это можно изобразить в терминах Теории Категорий?
Все, что я могу изобрести это три штуки и их комбинацию: domain, codomain, arrow. Кроме того, у нас есть простая структура {old -> 2; new ->2}.
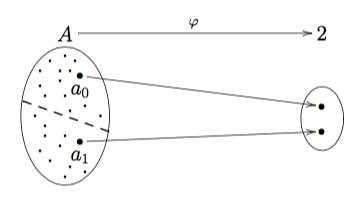
Для описания состояния мира после изобретения велосипеда нам надо перемножить эти конструкции.
Допустим, велосипед - это новая стрелка f.
f(0): old domain -> old codomain
f(1): new domain -> old codomain
f(2): new domain -> new codomain
Получается, что в данном случае изобретение велосипеда - это изобретение фанктора.
Неверно, хотя идея соблазнительная.
Все, что я могу изобрести это три штуки и их комбинацию: domain, codomain, arrow. Кроме того, у нас есть простая структура {old -> 2; new ->2}.
Для описания состояния мира после изобретения велосипеда нам надо перемножить эти конструкции.
Допустим, велосипед - это новая стрелка f.
f(0): old domain -> old codomain
f(1): new domain -> old codomain
f(2): new domain -> new codomain
Неверно, хотя идея соблазнительная.
